はじめに
深層学習 (ディープラーニング) をはじめとした機械学習の発展を受けて、物理シミュレーションや実験といった製品の評価を機械学習モデルで代替する動きが盛んになってきました。機械学習を用いることで、製品の評価結果を高速に、または高精度に得ることができるようになってきています。
弊社においても物理シミュレーションの機械学習に関して研究開発を進めており、筑波大学と弊社の共同研究結果が機械学習のトップ国際会議のひとつである International Conference on Learning Representations (ICLR) に採択されました1。この記事では、当該論文を中心に、物理シミュレーションのための機械学習モデルについて解説します。なお、当該論文のソースコードは https://github.com/yellowshippo/isogcn-iclr2021 にて公開されています。
物理シミュレーションの機械学習をやる必要性
有限要素法 (FEM) をはじめとする物理シミュレーションは、製品の性能評価や製造プロセスの検証において重要な役割を果たしています。製品を製造して実測すると高額になることが多く、また実験結果として得られる情報も限られたものになってしまいます。一方で、物理シミュレーションを行うことにより、製造に関するコストをかけることなく評価結果が得られることに加え、実測では得られないような詳細な情報 (製品内部の温度分布や流体の流れ場など) を得ることができます。
しかしながら、正しい物理シミュレーションを行うためには長い計算時間がかかることがあるほか、計算結果が実験による計測データと乖離してしまうことがあるなど、物理シミュレーションそのものにも改善が必要なケースがみられます。これらの点が解決されれば、物理シミュレーションの適用範囲はより広いものとなり、ものづくりにより大きく貢献できると考えられます。
物理シミュレーションの改善にはさまざまな方法が考えられますが、機械学習も有力な手法のひとつです。例えば、従来のシミュレーション手法に比べて高速な機械学習モデルに置き換えることによって計算時間を高速化する (図 1 (a))、シミュレーション結果の代わりに実験結果を学習させることによって実験との乖離を低減する (図 1 (b)) などの活用法が考えられます。この記事では、特に機械学習による物理シミュレーションの高速化について説明していきます。
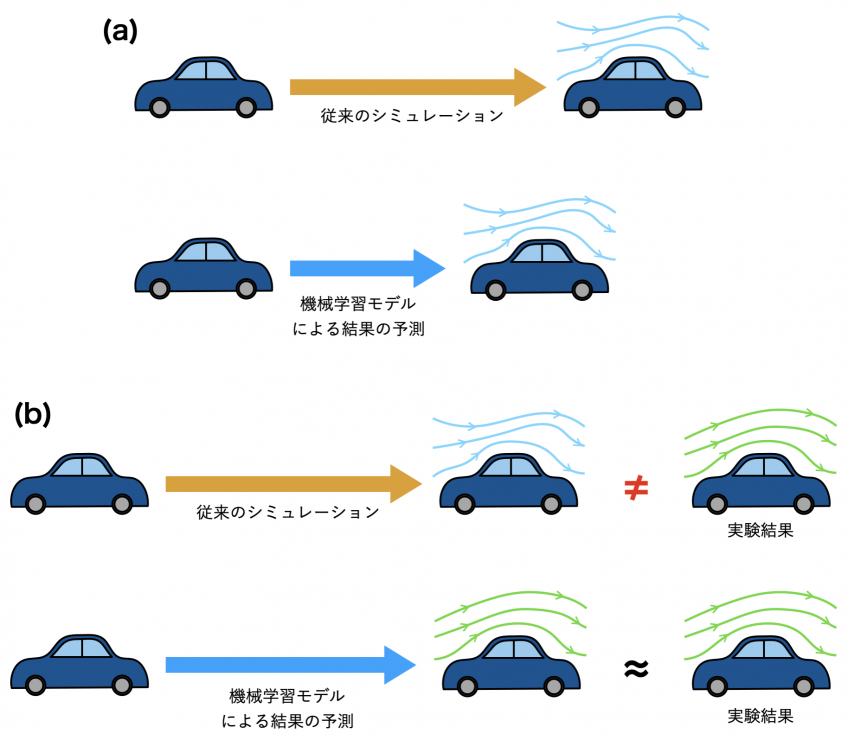
図 1: (a) 従来の物理シミュレーションを高速な機械学習モデルに置き換えた例および (b) 実験結果を予測する機械学習モデルの例
物理シミュレーションを学習するために必要なこと
物理シミュレーションを高速化するための機械学習モデルについて、以下の 3 点が必要であると考えられます:
- 工業製品にみられるような複雑形状を、情報を失わずに扱えること
- 予測をするための計算が高速であること
- 物理現象の特性を反映していること
1 つめの点は、「メッシュで表現されているデータを、画像等に変換することなくそのまま入力できること」とも言えます。そのためには、グラフニューラルネットワーク (GNN) と呼ばれる機械学習モデルを用いることが重要です。詳細に関しては、弊社の別の記事「FEM と幾何学の機械学習」を参照してください。
2 つめの点については、物理シミュレーションの高速化が目的の場合、必ず達成しなければならない条件となります。
3 つめの点について詳しく説明します。物理現象は、それを観測している座標系によらず本質的には同一なものとなります。例えば、ある物体の変形という同じ現象をある場所から見ている A さんと、別の場所から見ている B さんがいたとします。ふたりの間では見ている場所が違うので、B さんが見ている物体は A さんから見て回転や平行移動がなされた状態であると考えることができます。このとき、B さんから見た物体の変位は、A さんから見た変位に対して同じように回転がほどこされたものになります (図 2)。
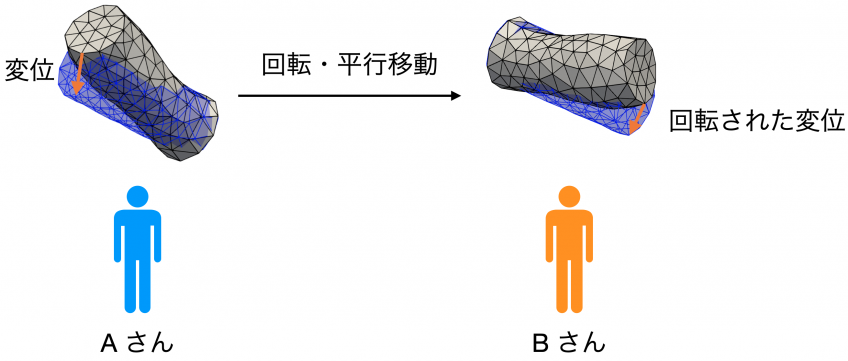
以上のことから、物理シミュレーションの結果を回転させたものは、入力を回転させて物理シミュレーションをした結果と同じになることがわかります。この性質を、回転・平行移動に関する 同変性 (equivariance) と呼びます。物理現象に登場する物理量はすべて同変性を持ちますので、この性質を正しく扱うことは、物理シミュレーションを機械学習する際にも重要となってきます。
しかしながら、残念なことに、ディープニューラルネットワークに代表される通常の機械学習モデルは同変性を持ちません。例えば 2 次元空間上のベクトル (1,0) を反時計回りに 90° 回転させたものは (0,1) となりますが、同変性がない機械学習モデルはこれらの「回転」という関係性には気づかずに、別の入力データとして取り扱われることとなり、したがって出力結果も同変性を持つことは保証されません。
つまり、ある座標系では精度が高い機械学習モデルでも、同じ入力データを座標変換したものを入力してしまうと精度が劣化してしまうということが起こってしまうかもしれないのです。工業製品では同じ部品が複数箇所に使われている場合があり (例えばネジなど)、入力データの座標変換は非常に頻繁に行われています。たくさんのネジが使われている製品があったときに、あるネジのまわりだけ突然精度が悪くなるおそれがあるような機械学習モデルでは、その結果をものづくりのための意思決定に反映させにくくなってしまいます。
もちろん、大量にデータを用意することによってデータから同変性を近似的に獲得することも不可能ではありません。しかし、回転や平行移動は連続的な変換であり、どの程度データを用意すればよいか不明であること、データ数が増えることにより学習に時間がかかることなどがデメリットとして挙げられます。したがって、同変性を持つ機械学習モデルを用いることが、ものづくりのために使いやすい機械学習モデルの要件であるといえます。
IsoGCN
前節の冒頭に掲げた、物理シミュレーションを高速化するための機械学習モデルの要件は、下記のように言い換えられます:
- メッシュデータを取り扱えるグラフニューラルネットワーク (GNN) であること
- 予測をするための計算が高速であること
- 回転・平行移動に関する同変性を持つこと
筑波大学と弊社の研究成果として提案された IsoGCN は、上記の条件をすべて満たします。IsoGCN は GNN をベースにしたモデルなので、メッシュの節点数や要素数が変わっても同じ機械学習モデルで対応することができ、高速に結果を予測することができ、そして同変性を持ちます。すなわち、IsoGCN は、物理シミュレーションを学習することに適したモデルであると考えられます。さらに、IsoGCN は微分を高精度に学習できることも示されています (図 3)。物理シミュレーションで扱われる支配方程式は微分方程式で記述されることが多いため、この性質は物理シミュレーションの機械学習にとって非常に有用なものとなります。
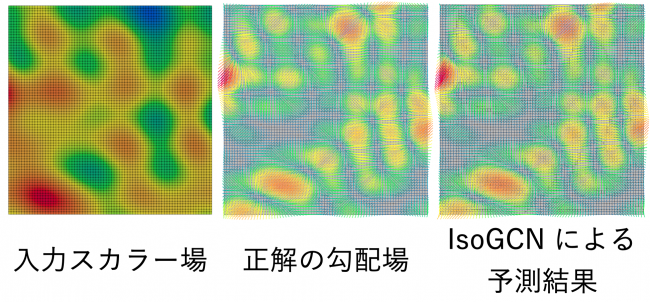
また、IsoGCN は熱拡散の問題に対しても、有限要素解析と比較して誤差 3 〜 5% 程度と高い精度で予測できています (図 4)。また、IsoGCN は有限要素解析ソフトウェアよりも高速に予測結果が出力できることも示されました。また、既存の同変性がある機械学習モデルでは予測にかかる時間が有限要素解析にかかる時間よりも長いため、IsoGCN が物理シミュレーションの機械学習にとって最も適切なモデルであることが示唆されています。
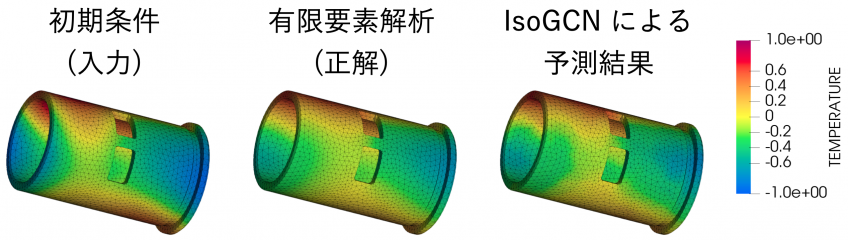
さらに、IsoGCN では 100 万節点ほどの巨大なメッシュに対しても問題なく結果を予測できることが示されています (図 5)。既存の同変性がある機械学習モデルでは、同じメッシュに対して 500GB のメモリがある計算機を使ってもメモリ不足になってしまいます。つまり、実問題で扱われるようなメッシュに対しても問題なく使用できるという意味でも、IsoGCN は物理シミュレーションの機械学習に適しています。
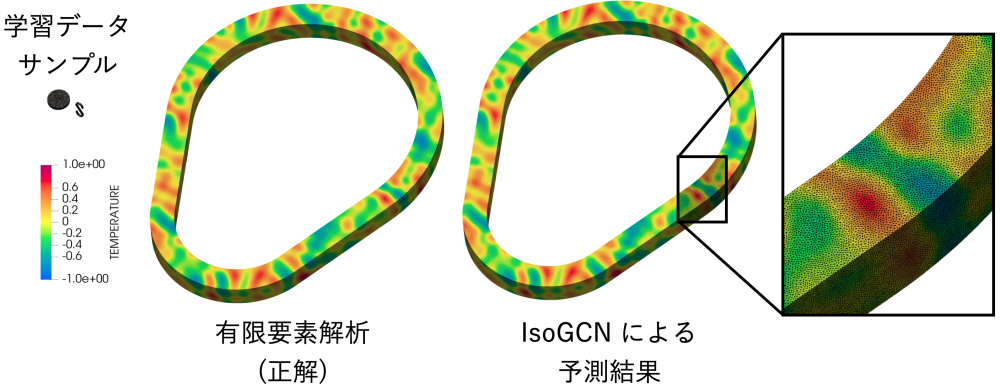
加えて、IsoGCN は形状に対する外挿を高精度に行うこともできます。比較的小さいメッシュでしか学習していなくても、巨大なメッシュに対して精度を劣化させることなく結果を予測できます (図 5)。これは、IsoGCN が同変性を持ち、データから物理現象の本質的な部分を正しく学習できているためであると考えられます。このように、学習対象に成り立つ法則性を機械学習モデルに付与することにより、高精度な扱いやすい機械学習モデルを構築することができます。
おわりに
この記事では、提案手法である IsoGCN が、物理シミュレーションを学習して高速化するために最適な機械学習モデルであることを解説しました。具体的には、以下のようにまとめることができます:
- グラフニューラルネットワーク (GNN) をベースにしているため、工業製品にみられるような複雑形状でも、情報を失わずに扱える
- 予測をするための計算が有限要素解析よりも高速である
- 物理現象の特性を反映しているため、形状についての外挿も精度よく行える
これらの結果は、物理学・計算工学・情報科学の知見を高度に融合した結果得られたものです。弊社ではこの技術をもとにさまざまな問題の物理シミュレーションを機械学習によって高度化しております。この記事に関するご質問やこういった問題に適用できないかなどのお問い合わせは [email protected] までお寄せください。
- M. Horie, N. Morita, T. Hishinuma, Y. Ihara, N. Mitsume. Isometric Transformation Invariant and Equivariant Graph Convolutional Networks, In International Conference on Learning Representations (ICLR), 2021. [arXiv] ↑







